Reverse Carnot Cycle Efficiency
An air conditioning device is working on a reverse Carnot cycle between the inside of a room at temperature \(T_2\) and the outside at temperature \(T_1\) > \(T_2\) with a monatomic ideal gas as the working medium. The air conditioner consumes the electrical power P. Heat leaks into the house according to the law \(\stackrel{.}{Q} = A(T_1 − T_2)\).
- Show that the efficiency of the air conditioner is \(η_{cool} = {T_2 \over T_1-T_2}\).
- Express the inside temperature \(T_2\) in terms of \(T_1\), A, and P.
Solution
1. Efficiency
In the reverse Carnot cycle, work is done to extract heat from one system and expel it into another via four processes, two isothermal and two isentropic (constant entropy).
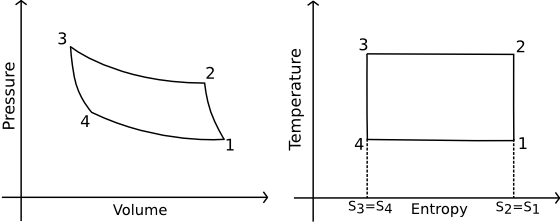
Reverse Carnot Engine. Source (now dead).
- In process \(1 \rightarrow 2\), the gas is isentropically compressed, and there is no heat flow into or out of the refrigerator.
- In process \(2 \rightarrow 3\), heat is expelled into the sink (e.g. outside air) isothermally (\(T_2\)=\(T_3\)). The amount of heat ejected per unit mass of gas is \(Q_C=T_2(S_2-S_3)\).
- In process \(3 \rightarrow 4\), the gas is isentropically expanded. The pressure and temperature decrease to \(P_4\), \(T_4\). Heat transfer at this stage is zero.
- In process \(4 \rightarrow 1\), the gas expands isothermally (\(T_4\)=\(T_1\)), extracting heat from the source (e.g. room).
This is where the cooling takes place. The heat extracted from the source per unit mass of gas is \[Q_H=T_1(S_1-S_4)=T_1(S_2-S_3).\]
The work done during the process is simply \[W=Q_H-Q_C=(T_1-T_2)(S_2-S_3).\]
The efficiency of the reverse Carnot cycle is the heat removed from the cold reservoir / the amount of work input: \(\eta_{cool}=\frac{Q_C}{W}\), so \[\eta_{cool}={T_2 \over T_1-T_2}\;\blacksquare \]
2. Express \(T_2\) in terms of \(T_1\), A, and P
Re-arranging \(\stackrel{.}{Q}\;\,=A(T_1 − T_2)\), we obtain \[T_2=T_1-{\stackrel{.}{Q} \over A}\] In equilibrium, the heat flow in \(\stackrel{.}{Q}\) must equal the power consumed \(P\) times the efficiency \(\eta\):1
\begin{eqnarray} T_2&=&T_1 – {P \eta \over A} \nonumber \\ &=&T_1 – {P T_2 \over A(T_1-T_2)} \nonumber \end{eqnarray}
This leads to a quadratic formula whose solution (taking the positive root) is:
\[T_2 = 2T_1+{P \over 2A}\bigg[\sqrt{{4 T_1 A \over P} + 1} - 1 \bigg]\;\blacksquare\]
-
Update (26/01/13): Sorry about the typo of the dropped η before; I’m sure you spotted it. ↩︎