Mandelstam Variables With Identical Particles
For the elastic scattering of identical particles, \(A + A → A + A\), what are the Mandelstam variables?
## Solution ##
The Mandelstam variables are defined, for a process \(1 + 2 → 3 + 4\), as
\begin{eqnarray} s &=& (p_1 + p_2)^2 \nonumber \\ t &=& (p_1 − p_3)^2 \nonumber \\ u &=& (p_1 − p_4)^2 \nonumber \end{eqnarray}
where the \(p\)s are the four-momenta.
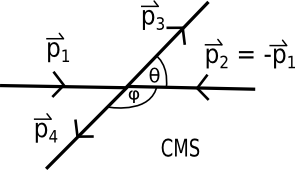
Relevant elastic collision for the \(t\) and \(u\) Mandelstam variables.
\(s\) variable
For the \(s\) variable, the scattering is something like two particles hitting each other head-on with \(\vec p_2=-\vec p_1\). We can calculate it for the case of identical particles like so: \begin{eqnarray} s = (p_1 + p_2)^2 &=& p_1^2+ 2p_1p_2 + p_2^2 \nonumber \\ &=& m_1^2 + 2p_1p_2 + m_2^2 \nonumber \\ &=& 2m_1^2 + 2(E_1E_2 − \vec p_1 \vec p_2) \nonumber \\ &=& 2m_1^2 + 2(E_1^2 + {\vec p_1}^2) \nonumber \\ &=& 2m_1^2 + 2\big((m_1^2 + {\vec p_1}^2) + {\vec p_1}^2\big) \nonumber \\ &=& 4(m^2 + \vec p^2) \end{eqnarray}
\(t\) variable
The relevant collision for the \(t\) variable is shown in the diagram. The momenta of particles 1 and 2 are equal and oppsite. Since they have the same mass, they must have the same energy too. After the collision, the particles again move with equal and opposite momentum, so \(E_1=E_2=E_3=E_4\) and \(|\vec p_1|=|\vec p_2|=|\vec p_3|=|\vec p_4|\). The calculation is at the bottom. The last relation \eqref{eq:lte} is true for any t-channel process.
\(u\) variable
The \(u\) variable is basically the same process as for the \(t\) variable, except the angle of scattering is \(\phi\) in the diagram instead of \(\theta\). This leads to the argument of the cosine being shifted by \(\pi\), thus changing its sign. Back to \(t\):
\begin{eqnarray} t=(p_1-p_3)^2&=& p_1^2 – 2p_1p_3 + p_3^2 \nonumber \\ &=& 2m_1^2 – 2E_1E_3 + 2 \vec p_1 \vec p_3 \nonumber \\ &=& 2m_1 – 2E_1^2 + 2 {\vec p_1}^2 \cos \theta \nonumber \\ \label{eq:lte} &=& -2 {\vec p}^2 (1-\cos \theta) \le 0 \end{eqnarray}
Therefore, for \(u\):
\begin{eqnarray} u=-2 {\vec p}^2 (1+\cos \theta) \end{eqnarray}